- · LFAToolkit.jl

Preconditioner: Multigrid

LFAToolkit supports both p-multigrid and h-multigrid.

LFAToolkit.MultigridType.MgridType — Type

Multigrid types

Types:

pmultigrid: p-multigrid
hmultigrid: h-multigrid

Example:

LFAToolkit.MultigridType.MgridType

# output
Enum LFAToolkit.MultigridType.MgridType:
pmultigrid = 0
hmultigrid = 1

source

P-Multigrid

Example

This is an example of a simple p-multigrid preconditioner.

# ------------------------------------------------------------------------------
# p-multigrid example
# ------------------------------------------------------------------------------

using LFAToolkit
using LinearAlgebra

# setup
mesh = Mesh2D(1.0, 1.0)
finep = 2
coarsep = 1
numbercomponents = 1
dimension = 2
ctofbasis = TensorH1LagrangeBasis(
    coarsep + 1,
    finep + 1,
    numbercomponents,
    dimension,
    collocatedquadrature = true,
)

# diffusion operators
finediffusion = GalleryOperator("diffusion", finep + 1, finep + 1, mesh)
coarsediffusion = GalleryOperator("diffusion", coarsep + 1, finep + 1, mesh)

# Chebyshev smoother
chebyshev = Chebyshev(finediffusion)

# p-multigrid preconditioner
multigrid = PMultigrid(finediffusion, coarsediffusion, chebyshev, [ctofbasis])

# compute operator symbols
A = computesymbols(multigrid, [3], [1, 1], [π, π])
eigenvalues = real(eigvals(A))

# ------------------------------------------------------------------------------

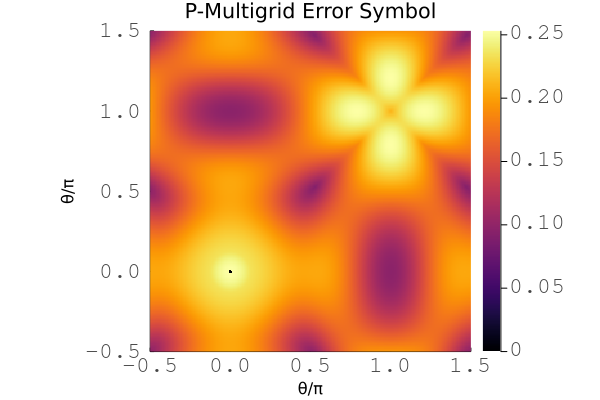
Example plot for the symbol of p-multigrid with a cubic Chebyshev smoother for the 2D scalar diffusion problem with cubic basis.

This is an example of a multilevel p-multigrid preconditioner.

# ------------------------------------------------------------------------------
# p-multigrid multilevel example
# ------------------------------------------------------------------------------

using LFAToolkit
using LinearAlgebra

# setup
mesh = Mesh2D(1.0, 1.0)
finep = 4
midp = 2
coarsep = 1
numbercomponents = 1
dimension = 2
ctombasis =
    TensorH1LagrangePProlongationBasis(coarsep + 1, midp + 1, numbercomponents, dimension)
mtofbasis =
    TensorH1LagrangePProlongationBasis(midp + 1, finep + 1, numbercomponents, dimension)

# diffusion operators
finediffusion = GalleryOperator("diffusion", finep + 1, finep + 1, mesh)
middiffusion = GalleryOperator("diffusion", midp + 1, finep + 1, mesh)
coarsediffusion = GalleryOperator("diffusion", coarsep + 1, finep + 1, mesh)

# Chebyshev smoothers
finechebyshev = Chebyshev(finediffusion)
midchebyshev = Chebyshev(middiffusion)

# p-multigrid preconditioner
midmultigrid = PMultigrid(middiffusion, coarsediffusion, midchebyshev, [ctombasis])
multigrid = PMultigrid(finediffusion, midmultigrid, finechebyshev, [mtofbasis])

# compute operator symbols
A = computesymbols(multigrid, [3], [1, 1], [π, π])
eigenvalues = real(eigvals(A))

# ------------------------------------------------------------------------------

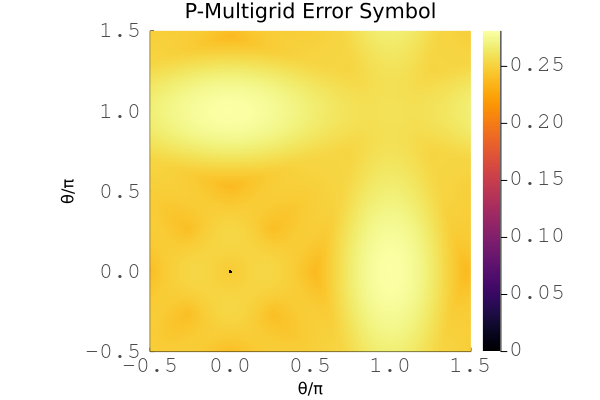
Example plot for the symbol of multilevel p-multigrid with a cubic Chebyshev smoother for the 2D scalar diffusion problem with cubic basis.

Documentation

LFAToolkit.PMultigrid — Function

Pmultigrid(fineoperator, coarseoperator, smoother, prolongationbases)

P-Multigrid preconditioner for finite element operators

Arguments:

fineoperator::Operator: finite element operator to precondition
coarseoperator::Union{Operator,Multigrid}: coarse grid representation of finite element operator to precondition
smoother::AbstractPreconditioner: error relaxation operator, such as Jacobi
prolongationbases::AbstractArray{<:AbstractBasis}: element prolongation bases from coarse to fine grid

Returns:

p-multigrid preconditioner object

Example:

# setup
mesh = Mesh2D(1.0, 1.0);
ctofbasis = TensorH1LagrangePProlongationBasis(3, 5, 1, 2);

# operators
finediffusion = GalleryOperator("diffusion", 5, 5, mesh);
coarsediffusion = GalleryOperator("diffusion", 3, 5, mesh);

# smoother
jacobi = Jacobi(finediffusion);

# preconditioner
multigrid = PMultigrid(finediffusion, coarsediffusion, jacobi, [ctofbasis]);

# verify
println(multigrid)
println(multigrid.fineoperator)

# output

p-multigrid preconditioner
finite element operator:
2d mesh:
    dx: 1.0
    dy: 1.0

2 inputs:
operator field:
  tensor product basis:
    numbernodes1d: 5
    numberquadraturepoints1d: 5
    numbercomponents: 1
    dimension: 2
  evaluation mode:
    gradient
operator field:
  tensor product basis:
    numbernodes1d: 5
    numberquadraturepoints1d: 5
    numbercomponents: 1
    dimension: 2
  evaluation mode:
    quadratureweights

1 output:
operator field:
  tensor product basis:
    numbernodes1d: 5
    numberquadraturepoints1d: 5
    numbercomponents: 1
    dimension: 2
  evaluation mode:
    gradient

source

LFAToolkit.computesymbols — Method

computesymbols(multigrid, p, v, θ)

Compute or retrieve the symbol matrix for a Jacobi preconditioned operator

Arguments:

multigrid::Multigrid: multigrid preconditioner to compute symbol matrix for
p::Array{Real}: smoothing paramater array
v::Array{Int}: pre and post smooths iteration count array, 0 indicates no pre or post smoothing
θ::Array{Real}: Fourier mode frequency array (one frequency per dimension)

Returns:

symbol matrix for the multigrid preconditioned operator

Example:

using LinearAlgebra

for dimension = 1:3
    # setup
    mesh = []
    if dimension == 1
        mesh = Mesh1D(1.0)
    elseif dimension == 2
        mesh = Mesh2D(1.0, 1.0)
    elseif dimension == 3
        mesh = Mesh3D(1.0, 1.0, 1.0)
    end
    ctofbasis = TensorH1LagrangeBasis(3, 5, 1, dimension; collocatedquadrature = true)

    # operators
    finediffusion = GalleryOperator("diffusion", 5, 5, mesh)
    coarsediffusion = GalleryOperator("diffusion", 3, 5, mesh)

    # smoother
    jacobi = Jacobi(finediffusion)

    # preconditioner
    multigrid = PMultigrid(finediffusion, coarsediffusion, jacobi, [ctofbasis])

    # compute symbols
    A = computesymbols(multigrid, [1.0], [1, 1], π * ones(dimension))

    # verify
    eigenvalues = real(eigvals(A))
    if dimension == 1
        @assert maximum(eigenvalues) ≈ 0.64
    elseif dimension == 2
        @assert maximum(eigenvalues) ≈ 0.9082562365654528
    elseif dimension == 3
        @assert maximum(eigenvalues) ≈ 1.4359882222222669
    end
end

# output

source

H-Multigrid

Example

This is an example of a simple h-multigrid preconditioner.

# ------------------------------------------------------------------------------
# h-multigrid example
# ------------------------------------------------------------------------------

using LFAToolkit
using LinearAlgebra

# setup
mesh = Mesh2D(1.0, 1.0)
p = 1
numbercomponents = 1
numberfineelements1d = 2
dimension = 2
ctofbasis = TensorH1LagrangeHProlongationBasis(
    p + 1,
    numbercomponents,
    dimension,
    numberfineelements1d,
);

# operators
finediffusion =
    GalleryMacroElementOperator("diffusion", p + 1, p + 2, numberfineelements1d, mesh);
coarsediffusion = GalleryOperator("diffusion", p + 1, p + 2, mesh);

# Chebyshev smoother
chebyshev = Chebyshev(finediffusion)

# h-multigrid preconditioner
multigrid = HMultigrid(finediffusion, coarsediffusion, chebyshev, [ctofbasis])

# compute operator symbols
A = computesymbols(multigrid, [3], [1, 1], [π, π])
eigenvalues = real(eigvals(A))

# ------------------------------------------------------------------------------

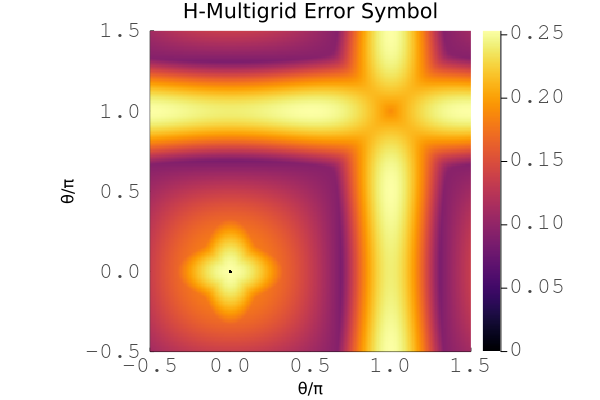
Example plot for the symbol of h-multigrid with a cubic Chebyshev smoother for the 2D scalar diffusion problem with linear basis.

This is an example of a multilevel h-multigrid preconditioner.

# ------------------------------------------------------------------------------
# h-multigrid multilevel example
# ------------------------------------------------------------------------------

using LFAToolkit
using LinearAlgebra

# setup
mesh = Mesh2D(1.0, 1.0)
p = 1
numberfineelements1d = 4
numbermidelements1d = 2
numbercomponents = 1
dimension = 2
ctombasis = TensorH1LagrangeHProlongationBasis(
    p + 1,
    numbercomponents,
    dimension,
    numbermidelements1d,
);
mtofbasis = TensorH1LagrangeHProlongationMacroBasis(
    p + 1,
    numbercomponents,
    dimension,
    numbermidelements1d,
    numberfineelements1d,
);

# operators
finediffusion =
    GalleryMacroElementOperator("diffusion", p + 1, p + 2, numberfineelements1d, mesh);
middiffusion =
    GalleryMacroElementOperator("diffusion", p + 1, p + 2, numbermidelements1d, mesh);
coarsediffusion = GalleryOperator("diffusion", p + 1, p + 2, mesh);

# Chebyshev smoothers
finechebyshev = Chebyshev(finediffusion)
midchebyshev = Chebyshev(middiffusion)

# h-multigrid preconditioner
midmultigrid = HMultigrid(middiffusion, coarsediffusion, midchebyshev, [ctombasis])
multigrid = HMultigrid(finediffusion, midmultigrid, finechebyshev, [mtofbasis])

# compute operator symbols
A = computesymbols(multigrid, [3], [1, 1], [π, π])
eigenvalues = real(eigvals(A))

# ------------------------------------------------------------------------------

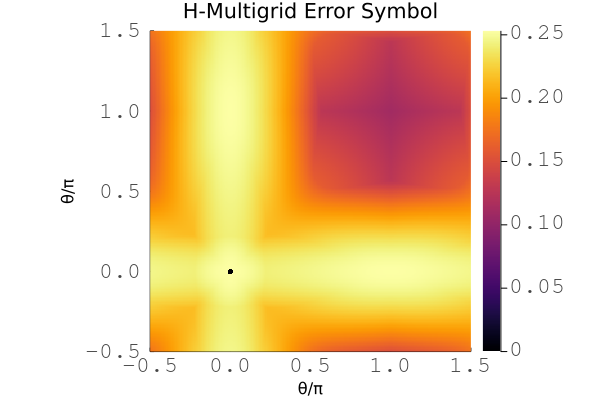
Example plot for the symbol of multilevel h-multigrid with a cubic Chebyshev smoother for the 2D scalar diffusion problem with linear basis.

Documentation

LFAToolkit.HMultigrid — Function

Hmultigrid(fineoperator, coarseoperator, smoother, prolongationbases)

H-Multigrid preconditioner for finite element operators

Arguments:

fineoperator::Operator: finite element operator to precondition
coarseoperator::Union{Operator,Multigrid}: coarse grid representation of finite element operator to precondition
smoother::AbstractPreconditioner: error relaxation operator, such as Jacobi
prolongationbases::AbstractArray{<:AbstractBasis}: element prolongation bases from coarse to fine grid

Returns:

h-multigrid preconditioner object

Example:

# setup
mesh = Mesh2D(1.0, 1.0);
ctofbasis = TensorH1LagrangeHProlongationBasis(2, 1, 2, 2);

# operators
function diffusionweakform(du::Array{Float64}, w::Array{Float64})
    dv = du * w[1]
    return [dv]
end
# -- fine
basis = TensorH1LagrangeMacroBasis(2, 3, 1, 2, 2);
inputs = [
    OperatorField(basis, [EvaluationMode.gradient]),
    OperatorField(basis, [EvaluationMode.quadratureweights]),
];
outputs = [OperatorField(basis, [EvaluationMode.gradient])];
finediffusion = Operator(diffusionweakform, mesh, inputs, outputs);
# -- fine
basis = TensorH1LagrangeBasis(2, 3, 1, 2);
inputs = [
    OperatorField(basis, [EvaluationMode.gradient]),
    OperatorField(basis, [EvaluationMode.quadratureweights]),
];
outputs = [OperatorField(basis, [EvaluationMode.gradient])];
coarsediffusion = Operator(diffusionweakform, mesh, inputs, outputs);

# smoother
jacobi = Jacobi(finediffusion);

# preconditioner
multigrid = HMultigrid(finediffusion, coarsediffusion, jacobi, [ctofbasis]);

# verify
println(multigrid)
println(multigrid.fineoperator)

# output

h-multigrid preconditioner
finite element operator:
2d mesh:
    dx: 1.0
    dy: 1.0

2 inputs:
operator field:
  macro-element tensor product basis:
    numbernodes1d: 3
    numberquadraturepoints1d: 6
    numbercomponents: 1
    numberelements1d: 2
    dimension: 2
  evaluation mode:
    gradient
operator field:
  macro-element tensor product basis:
    numbernodes1d: 3
    numberquadraturepoints1d: 6
    numbercomponents: 1
    numberelements1d: 2
    dimension: 2
  evaluation mode:
    quadratureweights

1 output:
operator field:
  macro-element tensor product basis:
    numbernodes1d: 3
    numberquadraturepoints1d: 6
    numbercomponents: 1
    numberelements1d: 2
    dimension: 2
  evaluation mode:
    gradient

source